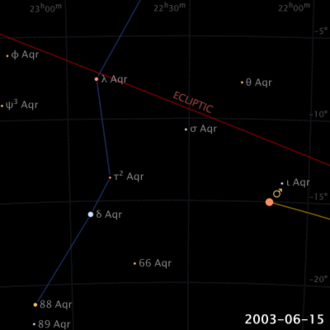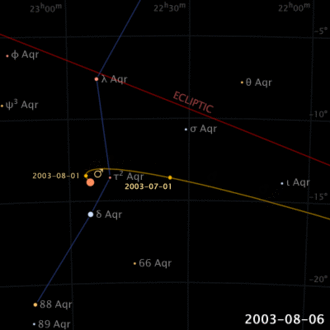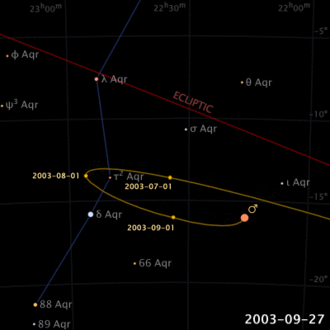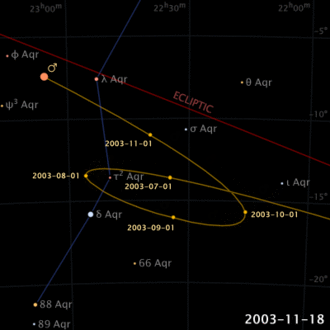
Schon in der Antike war es behannt dass, anders als Sonne und Mond, breschreiben Planeten komplizierte Bewegungen von Sternen zum Himmel (nicht zufällig bedeutet das Wort Planete, vom Griechen, “wandernd”). Sogar, ihre Bewegungsichtung scheint sich umzukehren, für einen bestimmten Zeitraum, und dann wieder in die eigene Richtung zu gehen (scheinbare rückläufige Bewegung).
Die geozentrische Modellen, dessen höchste Ausdrucksform das Tolematische Modell sein wird, deshalb mussten sie mehrere Korrekturen an der ursprünglichen Idee vornehmen, dass die Planeten einfach kreisförmig umkreisen, dessen Mittelpunkt die Position der Erde war.
Denn selbst philosophisch, war es damals unvorstellbar, dass Himmelskörpern auf anderen Pfaden als der Kreisbahn – Symbol für Perfektion – bewegten. Die Idee war, verschiedene Kreisbewegungen zu kombinieren. An der Basis aller Himmelsbewegungen wurden perfekte Kugeln vermutet. Dies wären vollkommen transparente Sphären, die sich gegenseitig ergänzen, und sich jeweils mit gleichbleibenden Drehgeschwindigkeit bewegten. Es wurde angenommen dass
ein hypothetischer Punkt, der sogennante Äquant, der eine in modo kreisförmige Bahn rund um die Erde gleichmässig beschreibt, die Deferent. Dieser Punkt, wiederum, war der Mittelpunkt einer anderen Kreisbahn, die Epyzikel gennant war, auf dem sich der Planet selbst bewegte.
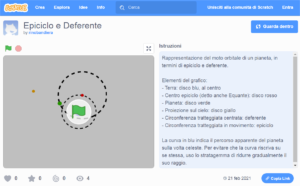
Das hier vorgestellte Modell (mit Scratch entwickelt) einfach dieses Konzept beschreibt. Die blaue Scheibe in der Mitte repräsentiert die Erde, und der gestrichelte konzentrische Umfang ist der Deferent. Der Äquant wird durch die rote Scheibe dargestellt, während die grüne Scheibe den Planeten repräsentiert, der sich durch Epizykel bewegt. Dies ist die kleinste gepunktete Zirrhose, immer zentriert auf dem Äquant.
Zu Beginn wird die Zeit der Planetenrevolution bestimmt (unter Bezugnahme auf das Heliozentrik-Modell). Wenn Sie lieber den Radius der Paneten-Umlaufbahn einstellen, dann geben Sie “R” ein. In diesem Fall ist R in Astronomischen Einheiten einzugeben, daß heißt in Einheiten des Erdumlaufradius. Größere Zeiträume oder Strahlungen als 1 beziehen sich auf externe Planeten, während Zeiträume oder Radien kleiner als 1 auf interne Planeten. Daher wird die Anzeigemodus angefordert, um su klären, wie das Bild des Planeten aussieht, das auf den Himmel projiziert wird. Ein Erdbeobachter kann nämlich nur die Proiektion der Position des Planeten, am Himmels messen, die hier als gelbe Scheibe dargestellt wird. Möglichkeiten sind: “V” um jederzeit den Vektor über de Planeten zu zeigen, oder “T” um die projizierte Bahn zu zeigen, die sich ständig formt, und den scheinbaren Pfad des Planeten zum Himmel darstellt. Um die scheinbare Flugbahn des Planetes schätzen zu können, ohne dass sich die Spur überschneidet, benutzen wir die Strategie, die Distanz der Projection schrittweise zu verringern. Dies dient natürlich nur der Veranschaulichung.
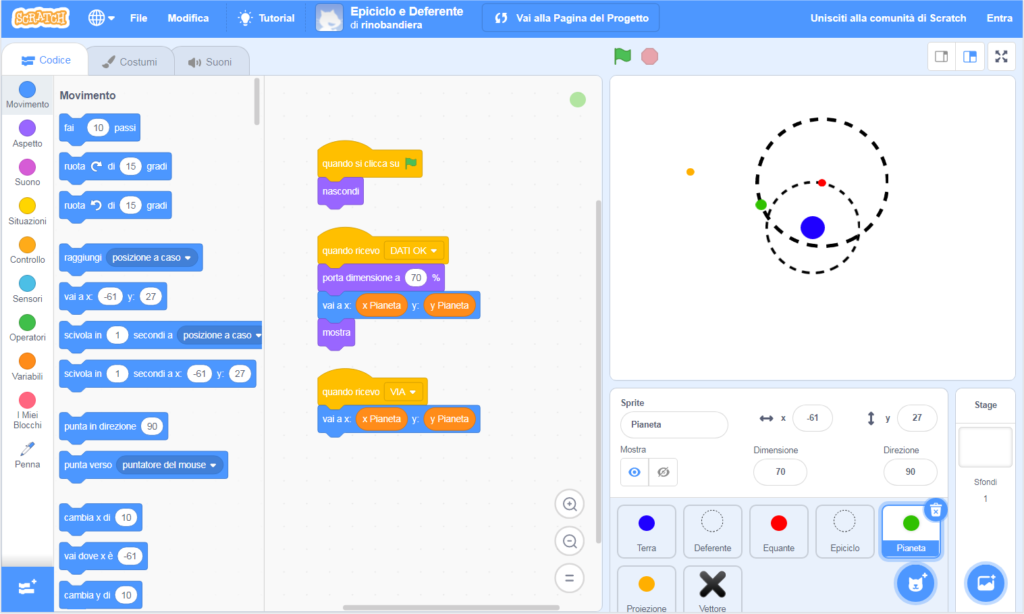
Schliesslich, einige Anmerkungen zum verwendeten Scratch-Code für dieses Modell. Zusätzlich zu den Spriten mit Platten Erde, Equante, Planet, und Projektion, für Epyzicle und Deferente verwenden wir zwei Sprite die, neben der gestrichelten Linie, sind transparent. Wir hätten ein einziges Sprite schaffen können, Equante+Epizykel, aber, aus Gründe der Kognition, haben wir es vorgezogen, diese getrennt. Zur effektiven Synchronisierung der verschieden Positionen, haben wir uns entschieden, den Coden am einem Ort – die Szene – zu sammeln. Nach ablesen der angegebenen Parameter, berechnet der Code die zeitliche Entwicklung der Positionen der einzelnen Komponenten.

Die Coden der verschiedenen Komponenten, beschränken sie sich darauf, sie nach der Dateneingabe zu erscheinen, und die Position der sich bewegenden Komponenten zu aktualisieren. Deswegen, wenn die Hauptcode die Dateneingabe-Phase beendet hat, die Nachricht “DATEN OK” sendet, um die verschiedene Sprite zu warnen, sich positionieren und auftreten. Danach, in jedem Zyklus – nach Neuberechnung aller Positionen – sendet der Hauptcode die Nachricht “WEG”, um die verschiedene Sprite zu warnen, ihre Positionen zu aktualisieren. Wir geben, beispielweise, den Planeten-Code:
Das vorgelegte Modell ermöglicht Ihnen einige Erfahrungen. Zum Beispiel, durch Einstellen von Zeit oder Radius größer als 1, simuliert es die Evolution für einen externen Planeten. Bei Werten unter 1, simuliert es die Evolution einnes Heimatplaneten. Im eristen Fall, werden Rückstrahlabschnitte auf die Erhöhung des Radius reduziert, während sie im zweiten Fall, bei Verringerung des Radius sinken. Interessant ist auch die Wirkung auf retrograde Bewegung zu bemerken, im Fall Radien in der Nähe von 1: sie werden größer, aber noch seltener sein. Schliesslich, stellen wir fest dass, für Perioden, bei denen es sich um Ganzzahlen oder Jahresbruchzahlen handelt, wird die Position der Hintergrundbewegungen in eine bestimmte Richtung am Himmel gerichtet.
Schliesslich, ist darauf hinzuweisen dass, die Epizyklus-Periode bleibt gleich wie das Erdjahr, während die Deferent-Periode wird gleich dem Jahr des Planetes sein, ebenso wie das Verhältnis der Epizyklus- und Deferent-Radien spiegelt in der Realität wieder, das Verhältnis der Orbitalradien der Erde und des Planeten. Natürlich ist alles klarer gemäss heliozentrischer Erklärung!
Zur Vertiefung:
