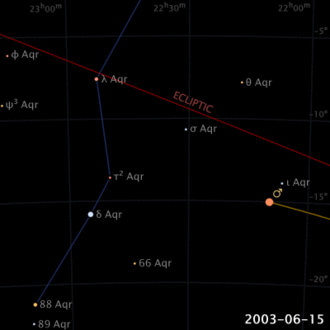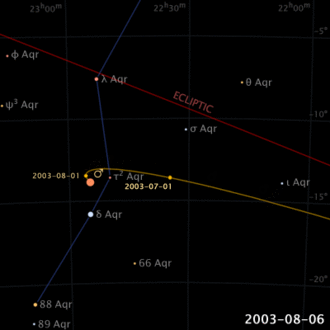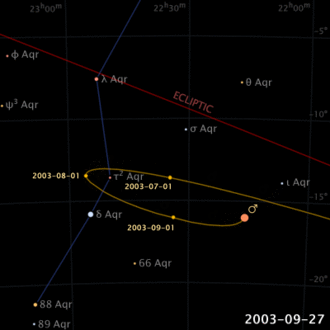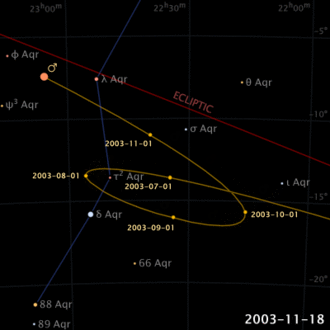
In ancient times it was already known that, unlike the Sun and the Moon, planets trace out complex motions in comparison with stars in the sky (not by chance, the word “pianet”, from the Greek, means “errant”). Even their direction of motion seems to be reversed, for a certain time, and then its direction is restored (apparent retrograde motion).
That is why the geocentric models, whose highest expression will be Ptolemy’s model, had to introduce various corrections to the originary idea, according to which planets simply orbit along circular trajectories whose centre was constituted by the Earth’s position.
Since, even according to the philosophy of that period, it was inconceivable that celestial bodies moved along trajectories other than the circle, symbol of perfection, the idea was to combine circular motions. At the base of all celestial motions there were supposed to be perfect spheres, which were perfectly transparent and, embedded in each other, and moved, each with a uniform rotation speed.
They supposed that an hypothetical point, called Equant, described a uniformly circular trajectory around the Earrth – the Deferent. This point, in turn, constituted the centre of another circular trajectory, the epicycle, on which the planet itself moved.
The model (developed with Scratch) presented here describes this concept in a simple way. The central blue disk represents the Earth, and the concentric dotted circumference is the Deferent. The Equant is represented by the red disk, whereas the green disk indicates the Planet, which moves along the Epicycle, the smaller dotted circumference, also centred on the Equant.
First of all, you must set the planet’s revolution period (in reference to the heliocentric model). On the other hand, if you prefer to set the radius of the planet’s orbit, enter “R”. In this case, R is therefore expressed in Astronomical units, namely in units of the Earth’s orbital radius. Periods, or radiuses higher than 1 refer to outer planets, whereas periods, or radiuses smaller than 1 refer to inner planets.
The display mode is then asked, so as to explain how the image of the planet projected upon the sky is formed. Indeed, an observer from the Earth can only measure the projection of the Planet’s position, on the celestial sphere, which is here represented by a yellow disk. The options are: “V” to show in each moment the vector passing through the planet , or “T” to show the projected trajectory being formed, which represents the apparent planet’s path on the celestial vault. In order to let you appreciate the planet’s apparent trajectory, without the trace overlapping in the drawing, we use the stratagem of gradually decreasing the distance of the projection. Obviously, this is done for illustrative purposes only.
Finally, some comments on the Scratch code used for this model. Over and above the sprites with disks representing the Earth, equant, planet, and its projection, for both the Epicycle and the Deferent, we use two sprites which, apart from the dotted line, are transparent. We could have created only one sprite, Equant+Epicycle, but for the sake of a clear presentation, we preferred to keep them separate. In order to effectively synchronize the various positions, we chose to gather in one single place – the stage – the code which, after reading the input parameters, calculates the evolution in time of the positions of the different components.

The codes of the various components only let them appear after the data input stage, and update the positions of the moving ones. That is why, when the main code completes the data input stage, it sends the message DATA OK, so as to inform the various sprites to take position and appear. Therefore, in each cycle – after calculating once again all positions – the main code sends the message GO, to inform the various sprites to update their own positions. We quote here, as an example, the planet’s code:
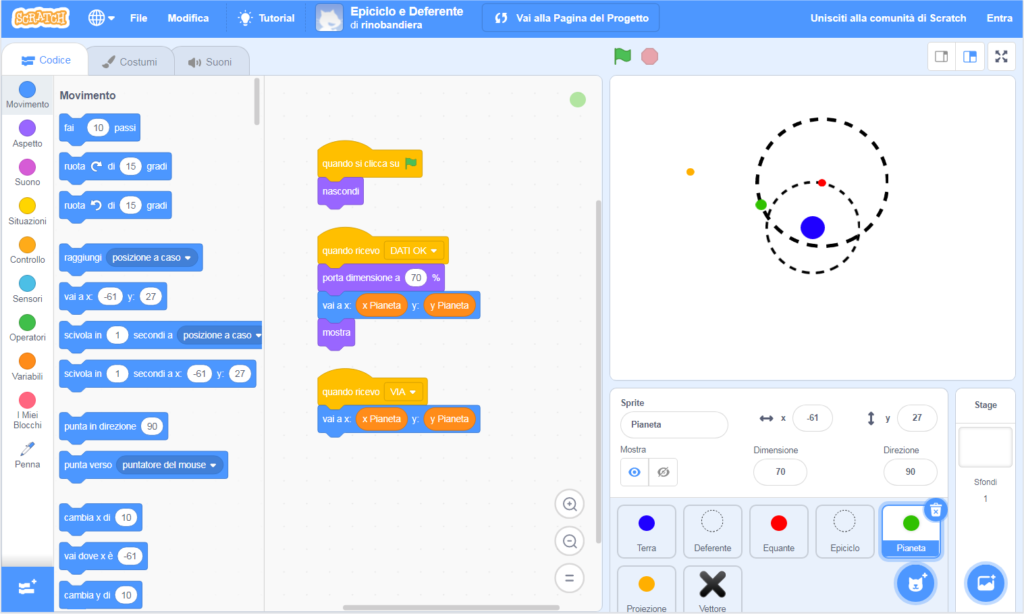
This modell allows you to carry out some experiences. For example, if you set a period, or radius, higher than 1, it simulates the evolution for an outer planet, whereas for values smaller than 1, the evolution of an inner planet. In the first case, the retrograde path sections are reduced with the increase of the radius, whereas in the second case, they are reduced with the decrease of the radius. It is also interesting to note the effects upon the retrograde motions in the case of radiuses near to 1: they will have a greater elongation, but will also be rarer. Finally, we can say that, for periods which are integers or simple fractions of the year, the positions of retrograde motions will be oriented in fixed directions of the sky.
Finally, we may note that the period of the Epicycle will always be equal to the Earth’s year, whereas the Deferent’s one will be equal to the planet’s yeas, just as the relationship between the Epicycle’s radiuses and the Deferent mirrors, in reality, the relationship between the Earth’s orbital radiuses and the ones of the planet in question. Obviously, everything is clearer if it is seen in a heliocentric explanation key!
For further information:
