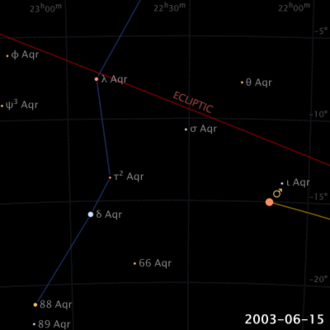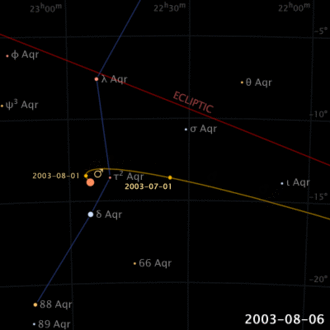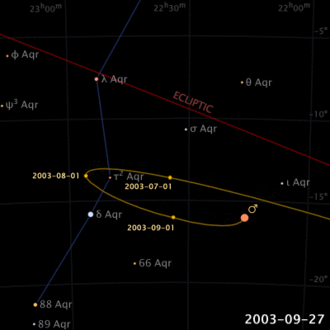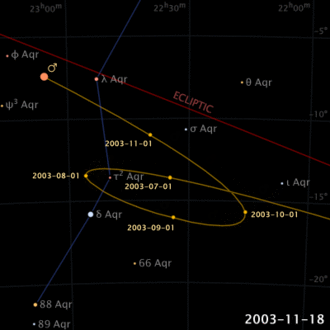
Déjà dans l’antiquiité il était connu que, contrairement au Soleil et à la Lune, les planètes décrivent des mouvements compliqués par rapport aux étoiles dans le ciel (pas par hazard le mot planète, du grec, signifie “errant”). Même leur direction de mouvement semble s’inverser, pendant une certaine période, pour ensuite rétablir sa propre direction (mouvement rétrograde apparent).
C’est pour ça que les modèles geocentriques, dont l’expression maximale sera ptolémaïque, ont du introduire différentes corrections à l’idée originale que les planètes orbitent simplement le long des trajectoires circulaires avec la Terre au centre.
Vu que, même philosophiquement, à l’epoque il était inconcevable que les corps célestes se déplacent dans des trajectoires autres que circulaire, symbole de perfecrtion, l’idée était de combiner des mouvements circulaires. À la base de tous les mouvements célestes, il était censé y avoir des sphères parfaites, parfaitement transparentes qui, enchâssées les unes sur les autres, se déplaçaient toutes avec une vitesse de rotation uniforme.
On supposait qu’un point hypothétique, dit Equant, décrivait de façon uniforme une trajectoire circulaire autour de la Terre, dite Déférente. Ce point, à son tour, constituait le centre d’une autre trajectoire circulaire, dite épicycle, sur la quelle la planète même se déplaçait.
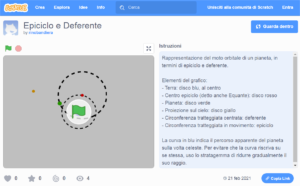
Le modèle (développé avec Scratch) présenté ici décrit simplement ce concept. Le disque bleu central répresente la Terre, et la circonférence pointillée – à lui concentrique – est la Déférente. L’Equant est representé par le disque rouge, tandis que le disque vert indique la Planète, qui se déplace le long de l’Épicycle, la circonférence pointillés plus petite, toujours centrée sur l’Equant.
Au début, il est demandé de définir la période de révolution de la planète (en se référant au modèle héliocentrique). Si vous préférez régler le rayon de l’orbite de la planète, entrez “R”. Dan ce cas, R doit donc être exprimé en Unités Astronomiques, c’est à dire en unités du rayon orbital terrestre. Périodes ou rayons supérieurs à 1 se rapportent à des planètes extérieures, tandis que des périodes ou des rayons inférieurs à 1 se référent à des planètes intérieures.
Le mode d’affichage est alors demandé, pour clarifier comment se forme l’image de la planète projetée sur le ciel. Un observateur de la Terre ne peut en effet que mésurer la projection de la position de la Planète, sur la sphère céleste, qui est representée ici par un disque jaune. Les options sont les suivantes: “V” pour montrer à tout moment le vecteur traversant la planète , ou “T” pour montrer la trajectoire projetée qui se forme lentement, et qui répresente le parcours apparent de la planète sur la voûte céleste. Pour permettre d’apprecier la trajectoire apparente de la planète, sans que la trace se chevauche dans le dessin, nous utilisont le stratagème de faire décroître graduellement la distance de la projection. Naturellement, ceci est à titre purement illustratif.
Enfin, quelques notes sur le code Scratch utilisé pour ce modèle réduit. En plus des sprites avec les disques répresentant la Terre, equant, planète, et sa projection, pour l’Epicycle et la Déferente utilisont deux sprites qui, à part la ligne pointillée, sont transparents. Nous aurions pu créer un seul sprite, Equant+Epicycle, mais pour être clair nous avons préferé les séparer. Pour synchroniser efficacement les différentes positions, nous avons choisi de recueillir en un seul endroit – la scène – le code qui, après avoir lu les paramètres entrés, calcule l’evolution dans le temps des positions des différentes composantes.

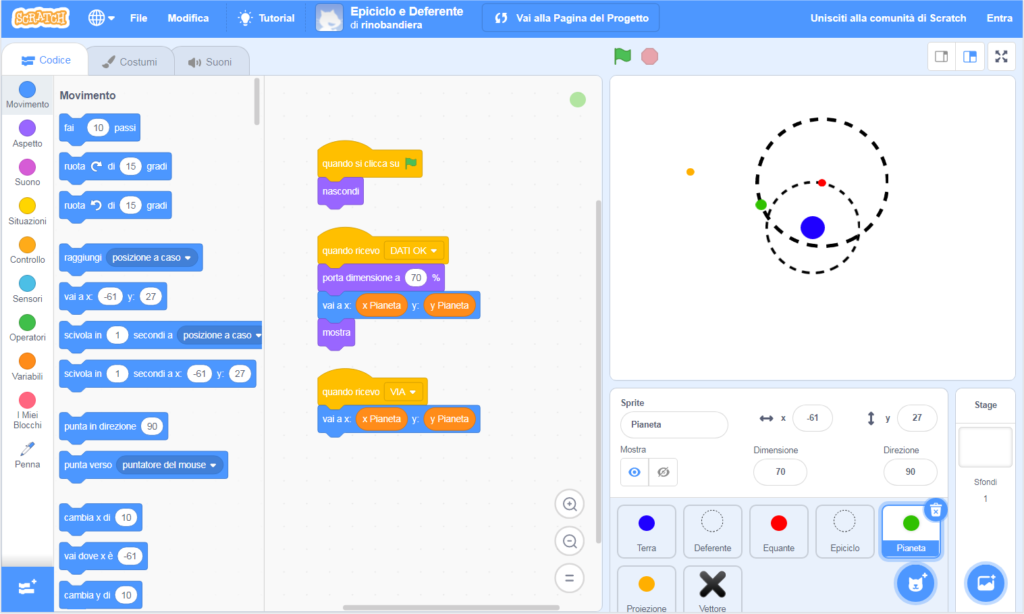
Les codes des différentes composantes se limitent à les faire apparaître après la phase de l’entrée des données, et à réactualiser les positions de celles en mouvement. Pour cela, quand le code principal a terminé la phase d’entrée des données, il envoie le messagge DONNÉES OK, pour avertir les différents sprites de se positionner et apparaître. Donc, à chaque cycle – après recalcul de toutes les positions – le code principal envoie le message ALLEZ, pour avertir les différents sprites de mettre à jour leurs positions. Nous reprenons, à titre d’exemple, le code de la planète:
Le modèle présenté permet de faire des expériences. Par exemple, avec le réglage d’une période – ou rayon – supérieure de 1 simule l’evolution pour une planète extérieure, tandis que pour des valeurs inférieures à 1, celle d’une planète intérieure. Dans le premier cas, les trajets rétrogrades se réduisent à l’augmentation du rayon, tandis que, dans le second cas, ils se réduisent à la diminution du rayon. Il est également interessant de noter les effets sur les mouvements rétrogrades dans le cas de rayons proches de 1: ils auront un allongement plus grand, mais ils seront encore plus rares. Enfin, on peut remarquer que, pour des périodes qui sont des valeurs entières, ou fractions simples de l’année, les positions des mouvements rétrogrades seront orientées dans des directions fixes du ciel.
On notera enfin, que la période de l’Epicycle sera toujours égale à l’année terrestre, tandis que celle de la Déferente sera égale à l’année de la planète, ainsi que le rapport entre les rayons d’Epicycle et Déferente reflète, dans la réalité, le rapport entre les rayons orbitaux de la Terre et de la planète en question. Évidemment tout est plus clair, si vu dans l’explication héliocentrique!
Pour approfondir:
