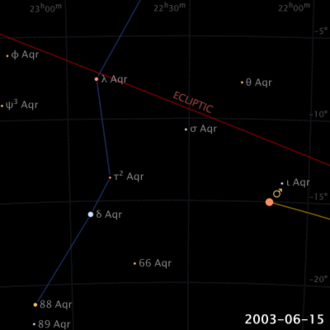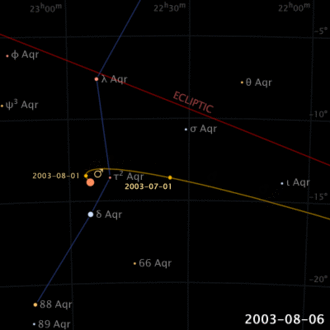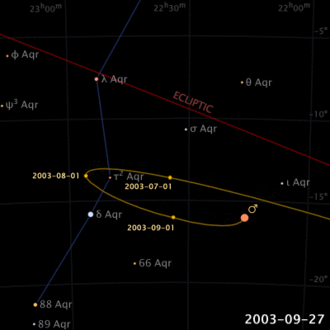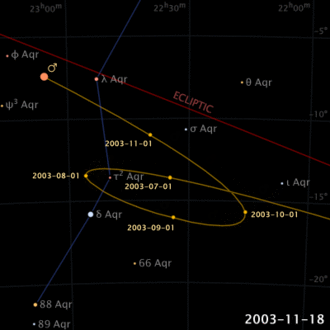
Già nell’antichità era noto che, a differenza del Sole e della Luna, i pianeti descrivono moti complicati rispetto alle stelle sulla volta celeste (non a caso la parola pianeta, dal greco, significa “errante”). Addirittura, la loro direzione di moto sembra invertirsi, per un certo periodo di tempo, per poi ristabilire la propria direzione (moto retrogrado apparente).
I modelli geocentrici, la cui massima espressione sarà il modello Tolemaico, per questo hanno dovuto introdurre varie correzioni all’idea originaria che i pianeti orbitassero semplicemente lungo traiettorie circolari di cui la posizione della Terra ne costituiva il centro.
Visto che, anche filosoficamente, all’epoca era inconcepibile che i corpi celesti si muovessero lungo traiettorie diverse da quella circolare, simbolo della perfezione, l’idea fu quella di combinare moti circolari. Alla base di tutti i moti celesti si supponeva vi fossero sfere perfette, perfettamente trasparenti che, incastonate le une alle altre, muovevano ognuna con velocità di rotazione uniforme.
Si suppose che un punto ipotetico, detto Equante, descrivesse in modo uniforme una traiettoria circolare attorno alla Terra, detta Deferente. Questo punto, a sua volta, costituiva il centro di un’altra traiettoria circolare, detta epiciclo, su cui si muoveva il pianeta stesso.
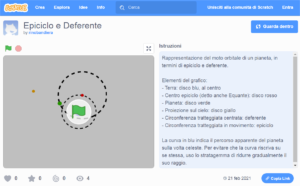
Il modellino (sviluppato con Scratch) qui presentato descrive in modo semplice questo concetto. Il disco blu centrale rappresenta la Terra e la circonferenza tratteggiata a esso concentrica è la Deferente. L’Equante è rappresentato dal disco rosso, mentre il disco verde indica il Pianeta, che si muove lungo l’Epiciclo, la circonferenza tratteggiata più piccola, sempre centrata sull’Equante.
All’inizio viene chiesto di impostare il periodo di rivoluzione del pianeta (facendo riferimento al modello eliocentrico). Se si preferisce invece impostare il raggio dell’orbita del pianeta, digitare “R”. In tal caso R andrà quindi espresso in Unità Astronomiche, cioè in unità del raggio orbitale terrestre. Periodi o raggi maggiori di 1 si riferiscono a pianeti esterni, mentre periodi o raggi minori di 1 a pianeti interni.
Viene quindi chiesta la modalità di visualizzazione, per chiarire come si forma l’immagine del pianeta proiettata sul cielo. Un osservatore dalla Terra infatti riesce a misurare solo la proiezione della posizione del Pianeta, sulla sfera celeste, che è qui rappresentata da un disco giallo. Le opzioni sono: “V” per mostrare in ogni momento il vettore passante per il pianeta , o “T” per mostrare la traiettoria proiettata che si va man mano formando, e che rappresenta il percorso apparente del pianeta sulla volta celeste. Per consentire di apprezzare la traiettoria apparente del pianeta, senza che la traccia vada a sovrapporsi nel disegno, usiamo lo stratagemma di far decrescere gradualmente la distanza della proiezione. Ovviamente, questo a puro scopo illustrativo.
Infine, alcune note sul codice Scratch utilizzato per questo modellino. Oltre agli sprite con i dischi che rappresentano Terra, equante, pianeta, e sua proiezione, per l’Epiciclo e la Deferente usiamo due sprite che, a parte la linea tratteggiata, sono trasparenti. Avremmo potuto creare un unico sprite, Equante+Epiciclo, ma per chiarezza espositiva abbiamo preferito tenerli separati. Per sincronizzare efficacemente le varie posizioni, abbiamo scelto di raccogliere in un solo posto – lo stage – il codice che, dopo aver letto i parametri immessi, calcola l’evolversi nel tempo delle posizioni delle varie componenti.

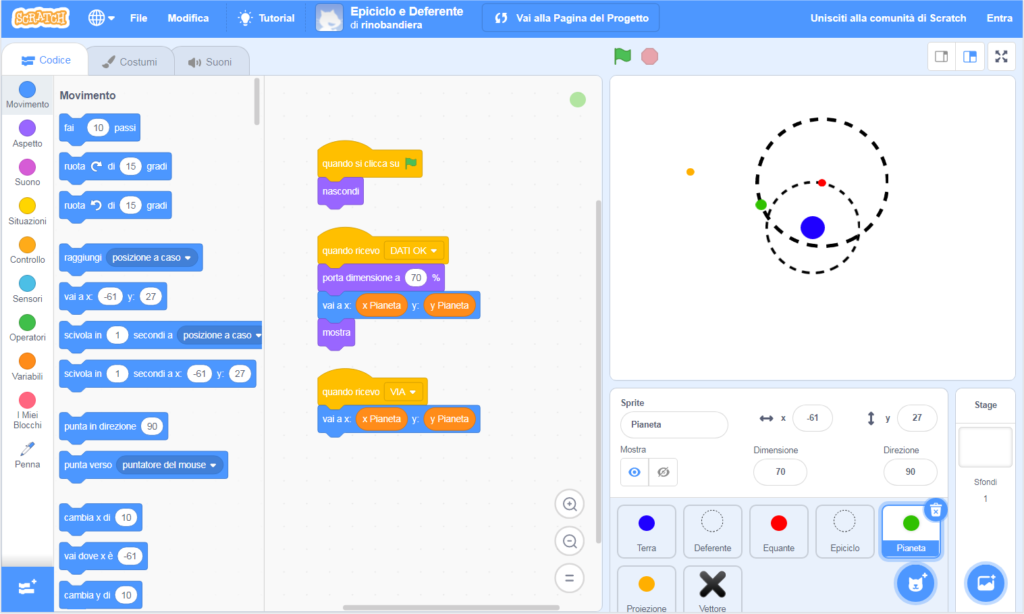
I codici delle varie componenti si limitano a farle comparire dopo la fase di immissione dati, e ad aggiornare le posizioni di quelle in movimento. Per questo, quando il codice principale ha terminato la fase di immissione dati invia il messaggio DATI OK, per avvertire i vari sprite di posizionarsi e apparire. Quindi, a ogni ciclo – dopo aver ricalcolato tutte le posizioni – il codice principale invia il messaggio VIA, per avvertire i vari sprite di aggiornare le proprie posizioni. Riportiamo, a titolo di esempio, il codice del pianeta:
Il modellino presentato consente di effettuare alcune esperienze. Ad esempio, impostando un periodo o raggio maggiore di 1 simula l’evoluzione per un pianeta esterno, mentre per valori minori di 1 quella di un pianeta interno. Nel primo caso i tratti di percorso retrogrado si riducono all’aumentare del raggio, mentre nel secondo caso si riducono al diminuire del raggio. Interessante anche notare gli effetti sui moti retrogradi nel caso di raggi vicini ad 1: essi avranno un’elongazione maggiore, ma saranno anche più rari. Infine possiamo notare come, per periodi che sono valori interi o frazioni semplici dell’anno, le posizioni dei moti retrogradi saranno orientate in direzioni fisse del cielo.
Da notare infine che il periodo dell’Epiciclo sarà sempre uguale all’anno terrestre, mentre quello della Deferente sarà uguale all’anno del pianeta, così come il rapporto fra i raggi di Epiciclo e Deferente riflette, nella realtà, il rapporto fra i raggi orbitali della Terra e del pianeta in questione. Ovviamente tutto risulta più chiaro se visto in chiave di una spiegazione eliocentrica!
Per approfondire:
