Negli ultimi decenni la scoperta e lo studio di pianeti che orbitano intorno a stelle diverse dal nostro Sole, detti esopianeti, hanno rappresentato una delle più affascinanti sfide scientifiche dell’astronomia moderna. Diversi telescopi spaziali hanno avuto un ruolo cruciale in questo campo, utilizzando principalmente il metodo dei transiti.
La prima missione che ha sfruttato questo metodo è stata Kepler (2009-2018), che ha permesso di scoprire migliaia di nuovi pianeti e di confermare che i sistemi planetari sono una regola più che un’eccezione nella nostra Galassia. A seguire, nel 2018, la missione TESS (Transiting Exoplanet Survey Satellite) della NASA ha proseguito e ampliato il lavoro di Kepler, concentrandosi sulla ricerca di pianeti attorno a stelle relativamente vicine e luminose.

Figura 1: Render del Telescopio Spaziale PLATO (credits: ESA)

La prossima tappa di questa esplorazione sarà la missione dell’Agenzia Spaziale Europea PLATO (PLAnetary Transits and Oscillations of stars). Selezionata nell’ambito del programma Cosmic Vision (M3), rappresenterà un significativo passo avanti nello studio degli esopianeti, con l’obiettivo principale di individuare pianeti terrestri situati nella zona abitabile intorno a stelle simili al Sole e di caratterizzarne le proprietà fisiche principali. Per raggiungere questo obiettivo, PLATO utilizzerà 26 telescopi da 20 cm di diametro, che insieme raccoglieranno la stessa quantità di luce di un unico telescopio da 1 metro, coprendo un campo visivo pari a 10.000 volte l’area apparente della Luna piena. PLATO osserverà simultaneamente migliaia di stelle, misurandone le variazioni di luminosità causate dai transiti planetari con una precisione senza precedenti.
Il metodo dei transiti sfrutta un principio semplice ma estremamente efficace: quando un pianeta transita, ossia passa davanti alla propria stella dal punto di vista di un osservatore, provoca una diminuzione della luminosità percepita. Questa variazione è tanto più evidente quanto maggiore è la dimensione del pianeta rispetto alla stella.
La misurazione accurata di questa diminuzione di luminosità permette di costruire una curva di luce, da cui è possibile ricavare importanti informazioni scientifiche:

  • Dimensione del pianeta: una diminuzione più pronunciata corrisponde a un pianeta più grande;
  • Periodo orbitale: la ripetizione periodica dei transiti consente di calcolare il tempo impiegato dal pianeta per compiere un’orbita completa.

Questi aspetti rendono il metodo dei transiti uno strumento potentissimo per la ricerca di nuovi esopianeti, non limitandosi alla semplice scoperta, ma offrendo la possibilità di approfondire la conoscenza delle caratteristiche fisiche dei pianeti individuati.

Derivazione formula per un sistema da banco

La variazione del flusso luminoso della stella osservata durante un transito può essere espressa quantitativamente attraverso una semplice relazione matematica. Supponendo che il pianeta e la stella abbiano entrambi forma sferica, la diminuzione relativa del flusso (ΔF/F) è data dal rapporto delle aree dei due corpi:

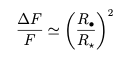
dove è il raggio del pianeta mentre  è il raggio della stella.

Questa semplice formula permette di determinare direttamente il raggio di un esopianeta, nota la diminuzione del flusso luminoso e il raggio della stella.
Dovendo però riprodurre il sistema stella-pianeta-osservatore in un sistema da banco (dimensioni tipiche (∼1 m) sono ∼8 ordini di grandezza inferiori rispetto alle scale tipiche del sistema solare (1 AU ≅1.5 ·10^8 m)), la domanda sorge spontanea: questa formula è ancora verificata?

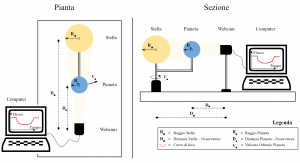
Figura 2: Rappresentazione schematica della configurazione sperimentale utilizzata.

Consideriamo una configurazione in cui, durante il transito, la stella e il pianeta sono allineati lungo la linea di vista dell’osservatore come riportato nella Figura 2. Il flusso di luce proveniente dalla stella sarà definito come:

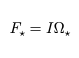
mentre il flusso osservato durante il transito sarà:

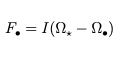dove e sono rispettivamente gli angoli solidi intercettati dall’osservatore relativamente alla stella e al pianeta, mentre I è l’intensità luminosa della stella. In questo caso possiamo definire l’angolo solido come:

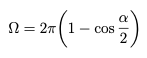
dove è la dimensione angolare della stella o del pianeta del punto di vista dell’osservatore. Da questa definizione, tramite qualche manipolazione trigonometrica, riportiamo la definizione di angolo solido in unità di lunghezza, ottenendo:

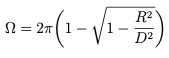
Quindi, sostituendo questa all’interno della definizione dei flussi otteniamo:

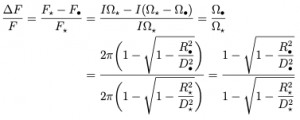
Nell’assunzione in cui le distanze stella-osservatore e pianeta-osservatore siano molto più grandi dei raggi (x=R/D<<1), espandendo in serie di Taylor (), si ottiene:

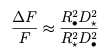
Infine, assumendo simile a torniamo alla formula iniziale:

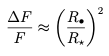
Materiale e Assemblaggio

La realizzazione del sistema stella-pianeta-osservatore richiede diversi componenti: alcuni possono essere stampati in 3D, alcuni facilmente acquistabili, ed altri strumenti comuni che si trovano facilmente a casa o in laboratorio.

Componenti stampabili in 3D:

  • Supporto in plastica per sfera Ø 20 cm (link progetto);
  • Supporto webcam (link progetto oppure qualunque sistema che tenga allineata la webcam al pianeta e alla stella);
  • Sfere opache di diverse dimensioni (link progetto oppure riproducibili con della carta argentata);
  • Asta in PVC 20 cm (link progetto).

Componenti da acquistare:

  • Sfera cava in PVC Ø 20 cm (link);
  • Supporto con motorino (link);
  • Led board con batteria (link).

Strumenti e materiali da avere a disposizione o acquistabili:

Figura 3: Modello da banco del sistema stella–pianeta
  • Computer;
  • Webcam;
  • Cacciavite;
  • 2 cavi con morsetti a coccodrillo;
  • Brugola;
  • Metro;
  • 6 bulloni;
  • 4 viti (1 cm);
  • 2 viti (0.5 cm);
  • 2 viti (3 cm);
  • Base circolare rigida (r = 5 cm)
  • Asta sottile (20 cm).
  • 2 batterie 1.5 V;
  • Multipack alimentazione motorino.

Posizioniamo dunque la base circolare rigida sul supporto con motore e assicuriamolo con le quattro viti da 1 cm utilizzando la brugola. Centriamo il supporto in PVC e assicuriamolo con quattro bulloni. Successivamente, posizioniamo la led board con alimentazione all’interno del supporto in PVC e assicuriamolo con due viti da 0.5 cm utilizzando il cacciavite. E’ importante accertarsi che i led siano rivolti verso l’alto. Fissiamo l’asta in PVC da 20 cm al supporto in plastica utilizzando le viti da 3 cm e i due bulloni rimanenti aiutandoci col cacciavite. Accendiamo i led dall’interruttore e posizioniamo la sfera in PVC Ø 20 cm sul supporto in plastica. Montiamo infine la webcam sul supporto e colleghiamola al computer.

Interfaccia utente Lightcurve

Per quanto riguarda la parte software, è possibile utilizzare il tool Lightcurve scaricabile gratuitamente su dispositivi con sistema operativo Windows.
L’interfaccia utente dell’applicazione è divisa in tre sezioni (dall’alto verso il basso):

  • Controlli e Impostazioni della fotocamera: può essere mostrata o nascosta cliccando sulla barra in alto. Di solito, questa sezione è necessaria solo per la configurazione iniziale e può essere nascosta durante la registrazione;
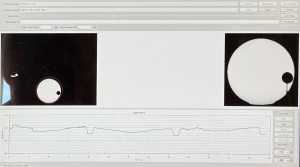
Figura 4: Interfaccia del software di acquisizione Lightcurve

 

  • Sezione immagine: qui vengono visualizzate due immagini, l’immagine originale della webcam e un ingrandimento del target selezionato;
  • Area grafico e controlli di registrazione: questa sezione mostra il grafico della curva di luce e consente di avviare/interrompere una registrazione. È possibile anche regolare l’area del grafico, resettarla ed esportarla come immagine o salvare i dati acquisiti in un file CSV.

Come effettuare la misura

Per eseguire una misura, posizioniamo l’asta sottile da 20 cm con una delle sfere nell’asta in PVC  assicuriamoci che il sistema sia ben centrato. Inseriamo le batterie da 1.5 V all’interno del multipack e colleghiamo le estremità dei fili servendoci dei cavi con morsetti a coccodrillo.
Misuriamo quindi le distanze stella-pianeta e stella-webcam utilizzando il metro e annotiamole in un quaderno. Una volta aperta l’applicazione Lightcurve dal computer selezioniamo la webcam dall’interfaccia e conntettiamola. Utilizziamo il menù a tendina per impostare la risoluzione desiderata dell’immagine, quindi clicchiamo su ‘Avvia‘ per avviare lo streaming delle immagini. Dal pulsante ‘Impostazioni‘ selezioniamo un cerchio di riferimento all’interno dell’immagine (tramite rilevamento automatico o controlli manuali). Se si desiderasse salvare un file video della registrazione, impostare il nome del file e il percorso e spuntare ‘Salva Filmato‘ se si vuole creare un file video. Se necessario, regolare il tempo e l’intervallo di luminosità dell’area del grafico. Avviare la registrazione della curva di luce e salvare i dati acquisiti una volta terminata l’acquisizione. L’applicazione misurerà la luminosità della sorgente in ogni fotogramma e la traccerà nel tempo sul grafico della curva di luce.