
Quando un corpo celeste non dotato di luce propria (come ad esempio un pianeta) passa di fronte a una stella, la luce che noi riceviamo da quella stella viene attenuata in proporzione alla frazione di area visibile che viene coperta dal pianeta. A seconda dei casi si può parlare di eclissi, di occultazione, o di transito.
Questo effetto si ha, ad esempio, quando la Luna passa davanti al Sole, dando luogo a quel fenomeno spettacolare noto come eclissi solare. Se la Luna arriva a coprire completamente il disco del Sole abbiamo una eclissi totale di Sole, ma questo accade molto raramente, in un luogo circoscritto della Terra, mentre è molto più frequente che il percorso della Luna sia decentrato rispetto al Sole, producendo una eclissi parziale.
Un caso particolare si ha quando la Luna, pur seguendo un percorso che incrocia il centro del Sole, si trova nella sua orbita a una distanza maggiore dalla Terra, quindi appare di dimensioni non sufficienti a coprire l’interno disco solare: in questo caso si ha una cosiddetta eclissi anulare. A parte il momento di massima eclissi – se non addirittura quello della totalità, che può durare solo alcuni minuti – l’intero fenomeno, dal momento in cui il disco lunare comincia a intaccare quello solare fino a quando ne riesce completamente, può durare molto più a lungo, fino a quasi due ore.
Siamo molto fortunati ad avere un satellite con dimensioni angolari vicine a quelle della nostra stella, perché questo ci permette di godere di una varietà di condizioni e di fenomeni altamente spettacolari! Se vivessimo su Marte, le eclissi solari da parte dei suoi satelliti, Phobos e Deimos, seppure visibili, sarebbero meno spettacolari (vedi ad esempio questo articolo su Media Inaf). Simili condizioni si hanno anche in molti altri casi, ma con effetti molto meno appariscenti. Ad esempio, nell’ambito del nostro Sistema solare, questo succede con il passaggio dei pianeti interni davanti al Sole, detti rispettivamente transito di Venere e transito di Mercurio.
Negli ultimi anni ha acquisito grande importanza lo studio dei transiti di pianeti extrasolari (detti anche esopianeti), perché rappresenta una delle tecniche per studiare sistemi planetari attorno ad altre stelle. Il passaggio di un pianeta davanti alla sua stella comporta una lieve diminuzione della luminosità apparente della stella stessa. Questa misurazione è estremamente difficile, ma anche estremamente utile, perché ci può permettere di stimare le dimensioni del pianeta, alcuni parametri della sua orbita, e perfino caratteristiche della sua atmosfera. Inoltre, da piccole variazioni del tempo di transito è possibile rivelare risonanze fra le orbite di vari pianeti, a causa della loro mutua attrazione gravitazionale, e da queste misurare perfino le masse dei singoli pianeti. Questo è stato possibile, ad esempio, con il sistema planetario attorno alla stella Trappist-1.
Schematizziamo la forma del pianeta e della sua stella come due cerchi perfetti. Inoltre trascuriamo eventuali differenze di luminosità sulla superficie della stella, come pure trascuriamo la presenza di un’atmosfera del pianeta. Il problema quindi si riduce a calcolare l’area dell’intersezione di due cerchi, un problema trigonometrico che in fondo non è molto complicato, se pensiamo che si tratta di calcolare l’area dei due segmenti circolari relativi ai due cerchi, i cui estremi corrispondono ai due punti di intersezione delle circonferenze; e l’area di ogni segmento circolare è semplicemente la differenza fra l’area del settore circolare e quella del triangolo con i medesimi vertici sulla circonferenza. La seguente animazione vuole rendere visivamente la geometria di questo problema (cliccare sul tasto PLAY per avviarla).
Con alcuni passaggi, è possibile calcolare i coseni dei due angoli al centro, rispettivamente della circonferenza 1 e di quella 2, come funzioni dei rispettivi raggi, R1 e R2, nonché della distanza h fra i loro centri:
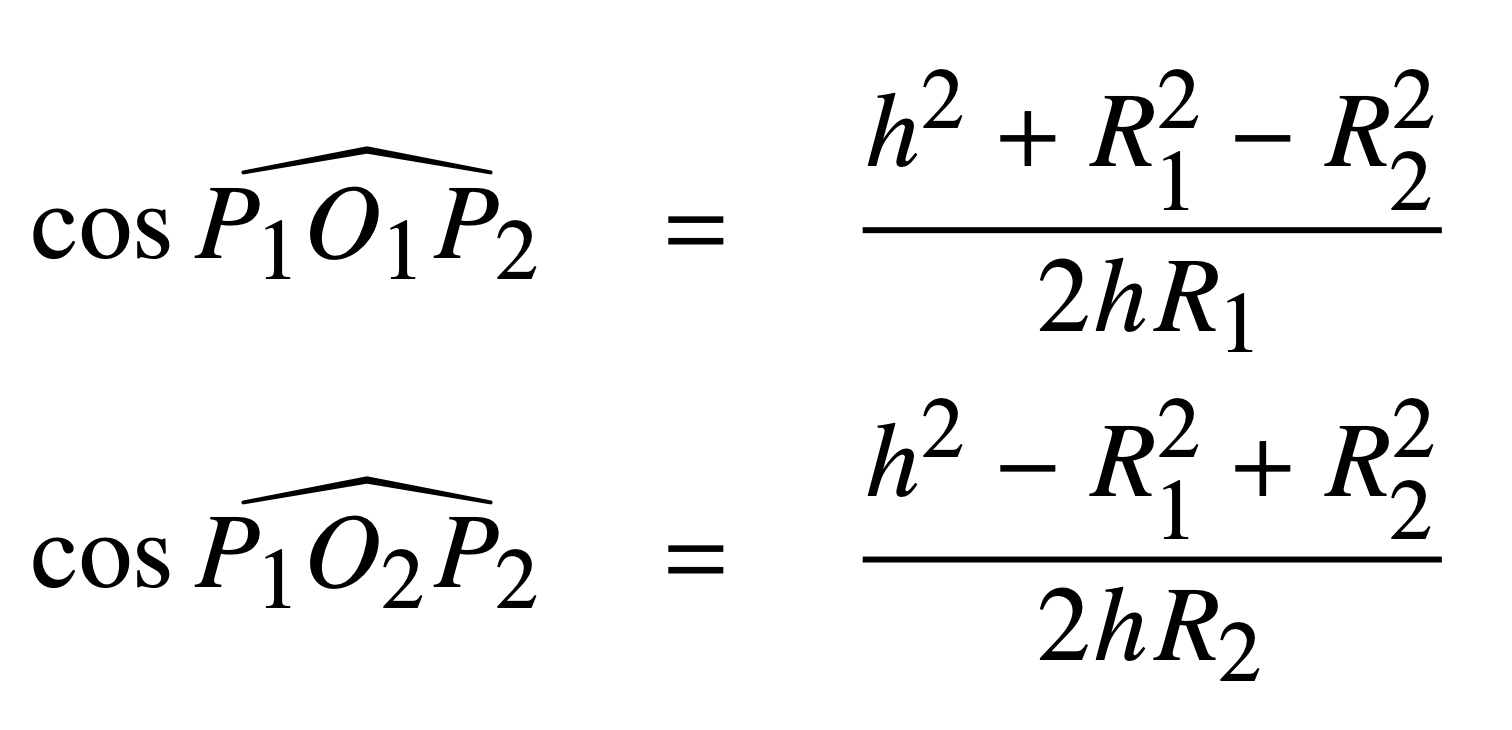
Ovviamente, in tutti i casi in cui non vi sono intersezioni, o i due cerchi sono esterni uno all’altro, oppure uno è completamente interno all’altro.
Il modello, sviluppato con Scratch e qui presentato, intende simulare gli effetti dei transiti di un pianeta davanti alla sua stella. Guardando dentro al progetto – in particolare il codice dello sprite Planet – è possibile vedere come è stato implementato l’algoritmo di calcolo del flusso osservato nei vari casi. Il calcolo è stato semplificato, schematizzando sia la stella che il pianeta come dischi circolari, e assumendo un’orbita circolare per il pianeta. Inoltre, sia i bordi della stella che quelli del pianeta sono considerati netti, senza la presenza di atmosfera.
Il progetto è stato sviluppato in modo da consentire di variare in modo interattivo alcuni parametri del modello: i raggi del pianeta e della stella (da 0 a 100, dove 100 corrisponde a metà raggio orbitale), l’inclinazione dell’orbita (da 0 a 100, dove 100 corrisponde ad un’inclinazione di 30 gradi), oltre a poter rallentare la visione del moto orbitale (per poter apprezzare meglio le fasi di inizio e fine del transito; anche qui selezionabili un valore da 0 a 100, in unità arbitrarie). Tutti questi parametri sono modificabili semplicemente agendo con il mouse sul cursore relativo ad ogni parametro, sullo schermo. Oltre a ciò, appare il valore istantaneo del flusso, in unità del flusso della stella quando non è occultata.
Nella parte inferiore del grafico, su uno sfondo nero, viene mostrato il grafico temporale dell’evoluzione in flusso. In altre parole, il grafico mostra – in tempo reale – il flusso osservato, in modo da poter esaminare le diverse strutture a seconda della geometria del sistema, passaggio completo o radente, e per vari rapporti fra i raggi della stella e del pianeta (il programma consente di impostare anche valori poco realistici, come un raggio del pianeta maggiore di quello della stella).
Per chi amasse non solo utilizzare ma anche modificare il codice, un esercizio interessante consiste nel simulare non un sistema stella + pianeta, ma una stella binaria a eclissi, il cui esempio più noto è la stella Algol, alias β Persei, cioè il caso in cui entrambi gli oggetti celesti sono luminosi. In tal caso (assumendo qui per semplicità che entrambi abbiano la stessa temperatura), il flusso totale sarà proporzionale all’unione delle due aree.
Per concludere, ecco qui una versione del programma in cui è stata data anche la possibilità di regolare il livello di rumore del segnale (noise). Ma perché peggiorare il segnale? Perché questo è ciò che succede comunemente nella realtà, che questo programma intende ad un qualche livello simulare. Le misurazioni, specialmente quando spinte ad un livello di accuratezza al limite delle possibilità strumentali, devono sempre confrontarsi con il problema del rumore, che può rendere imprecisi i valori misurati, o ancor peggio può mascherare completamente un effetto. In questo caso specifico è possibile sperimentare fino a quale livello, anche in presenza di rumore, una traccia del transito del pianeta è ancora apprezzabile ad occhio, e quando poi non lo è più.
Chi volesse assemblare un apparato che permetta di simulare in modo più concreto il transito di un pianeta, in questa scheda potrà trovare una descrizione dettagliata di un progetto Arduino che fa proprio questo.
Gli sprite utilizzati nel progetto sono stati disegnati da Barbara Olmi.
