Calcolo dinamico di un’orbita ellittica

Dopo aver sviluppato nei passi precedenti alcuni concetti geometrici sulle orbite ellittiche, ricaviamo ora traiettoria e legge oraria dell’orbita risolvendo esplicitamente le equazioni dinamiche, vale a dire la Seconda Legge di Newton e la Legge di Gravitazione Universale:

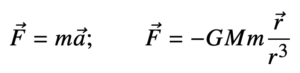
Queste in apparenza semplici leggi sono alla base di una vastissima complessità di moti. La prima equazione lega la forza applicata su un corpo e la sua accelerazione: questa è un’equazione vettoriale, e la costante m che lega le due grandezze è la massa dell’oggetto. La seconda (scritta qui nel caso speciale di due soli corpi), descrive una forza di attrazione proporzionale in modulo all’inverso del quadrato della distanza fra i corpi, e proporzionale al prodotto G·M·m, dove oltre alle masse dei due corpi compare G, la costante di gravitazione universale.

In questa sezione calcoleremo numericamente la rivoluzione di un pianeta attorno ad un corpo di massa M (la stella), che qui assumiamo molto maggiore di m e che quindi non si muoverà apprezzabilmente. Del caso di corpi con masse confrontabili parleremo in seguito. Combinando le due equazioni di cui sopra, entrambi lineari in m, si può vedere che il valore della massa m non influisce sul valore dell’accelerazione.

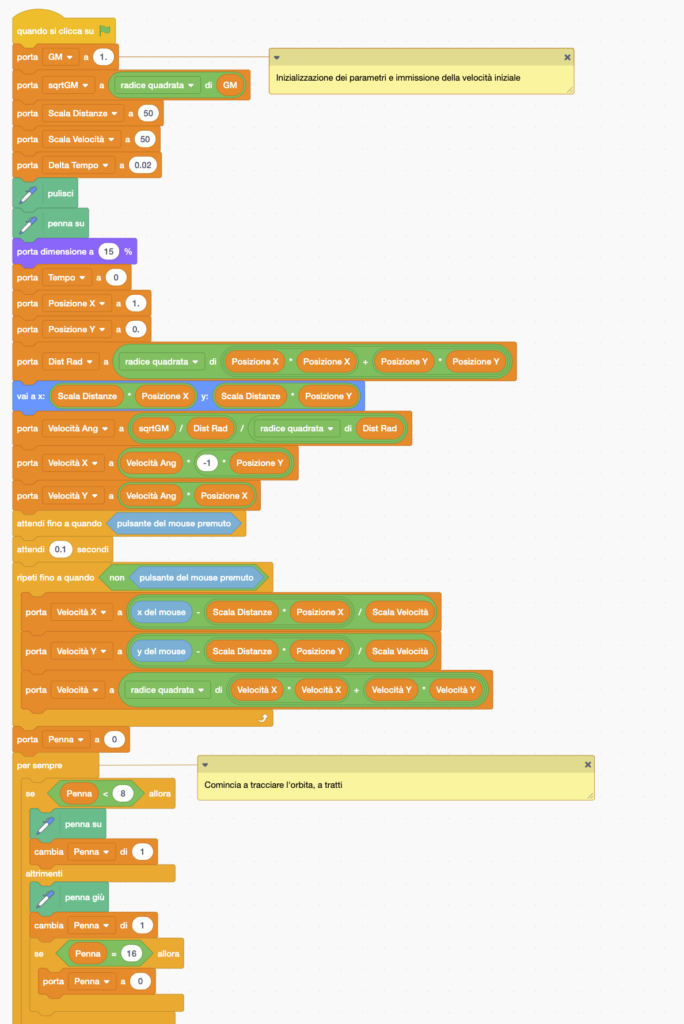
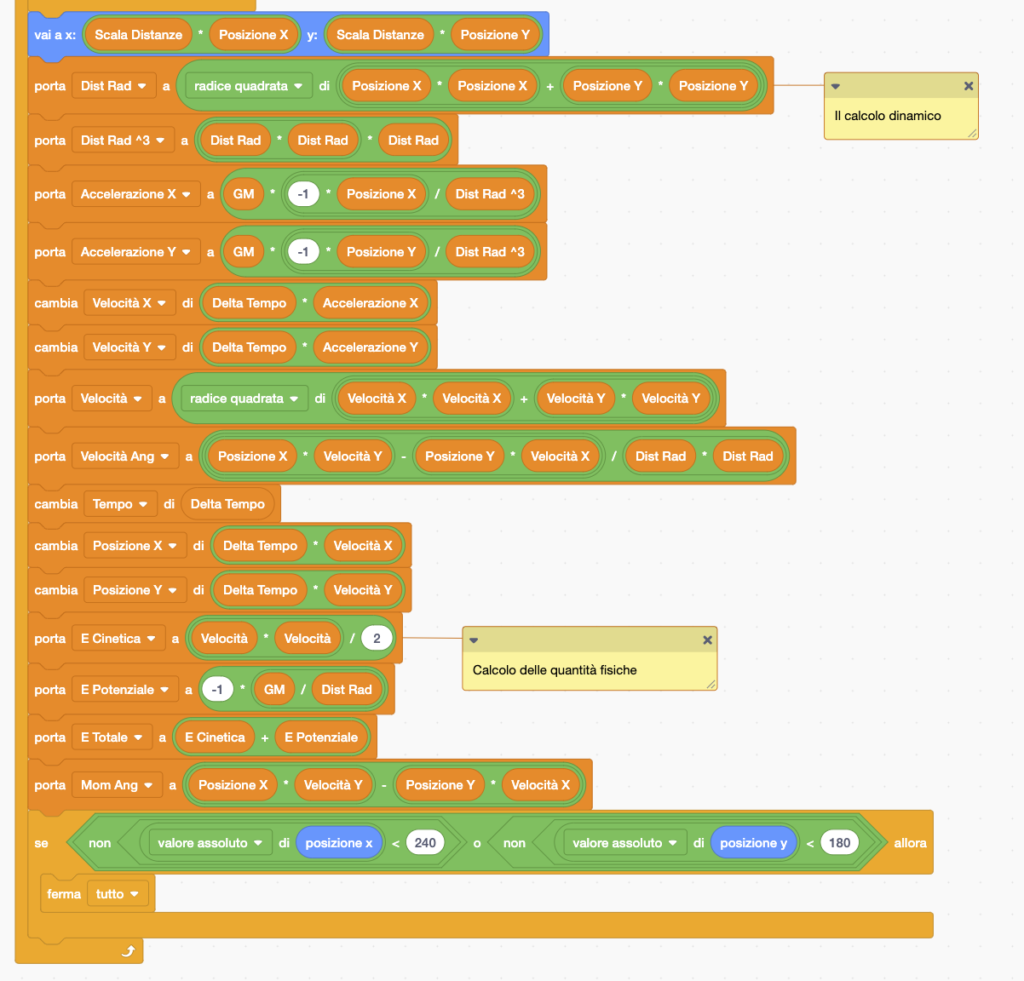
Veniamo ora al codice, dapprima in una forma semplificata:

Per scaricare il codice, o per eseguirlo, cliccare qui.

Questo codice eredita da quelli precedenti il metodo di immissione dati (interattivamente, con l’uso del mouse) per impostare la velocità iniziale. Inoltre, utilizza grandezze fisiche “normalizzate”, per quanto riguarda la distanza, la velocità, e la grandezza G·M (il prodotto della costante di gravitazione universale per la massa del corpo centrale).

Tanto per esemplificare, nel caso di un’orbita circolare con raggio = 1, per un valore di G·M = 1 la velocità orbitale sarebbe uguale a 1, la velocità angolare pure, in modo tale che il periodo orbitale sarà uguale a 2π, cioè circa 6.28 . Da notare che le variabili “Scala Distanze” e “Scala Velocità” hanno solo rilevanza per la visualizzazione grafica.

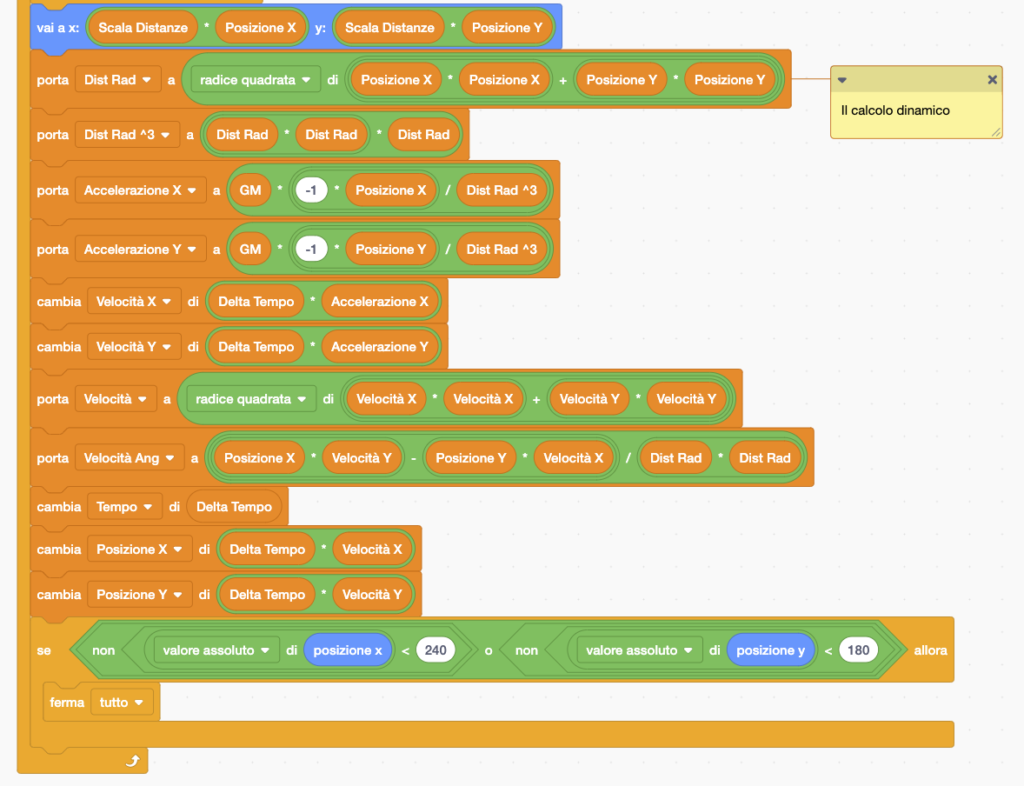
Per facilitare la scelta della velocità iniziale, all’inizio compare un punto nero che indica quale velocità andrebbe impostata per ottenere un’orbita circolare, mentre un segmento rosso, che cambia al variare della posizione impostata col mouse, rende conto di quale è la velocità impostata: una volta soddisfatti della scelta della velocità iniziale basta rilasciare il tasto del mouse e il programma comincia a calcolare ed a tracciare l’orbita stessa. Per far questo, usando la legge di gravitazione, calcola ad ogni tempo le componenti dell’accelerazione, e con queste aggiorna le componenti della velocità, ed infine la posizione del corpo.

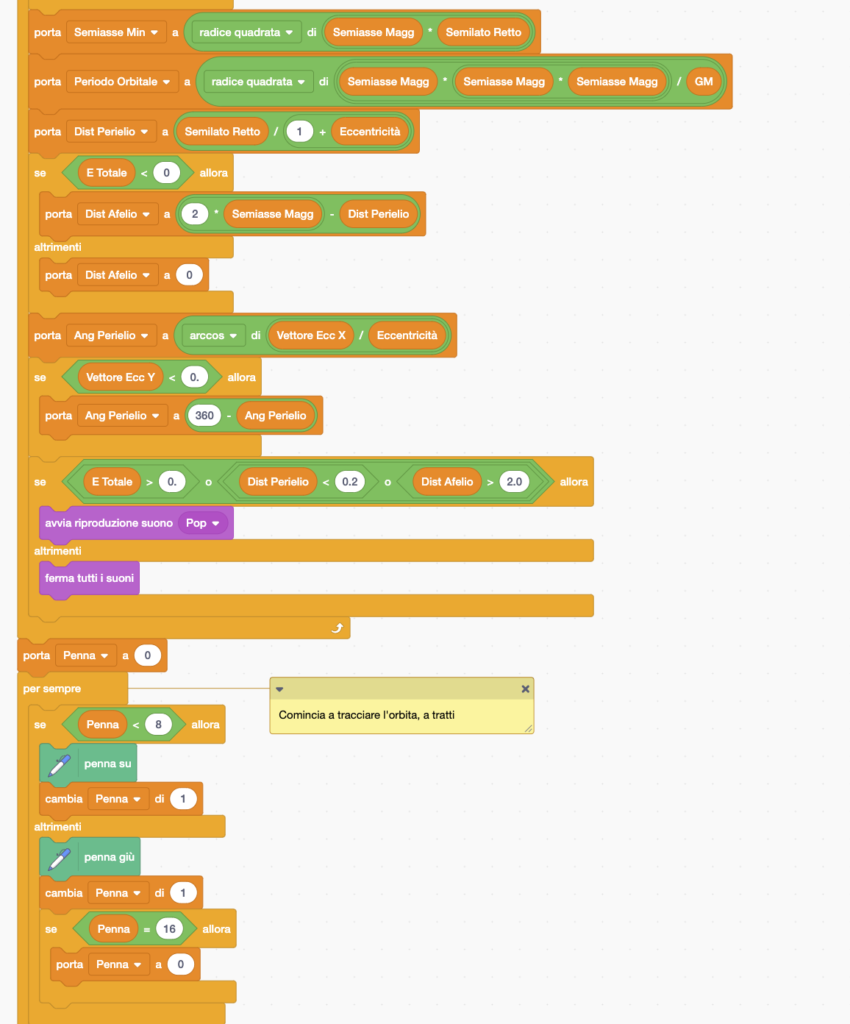
Nel visualizzare l’orbita percorsa viene usata una linea tratteggiata, con la penna su per un certo numero di cicli (nel programma, 8) e con la penna giù per altrettanti: questo per fornire un’idea di come cambia la velocità durante l’orbita. Ovviamente, dopo la prima orbita i tratteggi si andranno a sovrapporre.

Infine, un piccolo accorgimento consiste nel bloccare il programma nel caso in cui la posizione del corpo dovesse uscire dallo schermo. Se invece l’orbita rimane sempre all’interno dello schermo non è previsto nessuno stop automatico, ma l’esecuzione del programma dovrà alla fine essere bloccata manualmente.

Per approfondire:

Analisi di grandezze dinamiche e geometriche

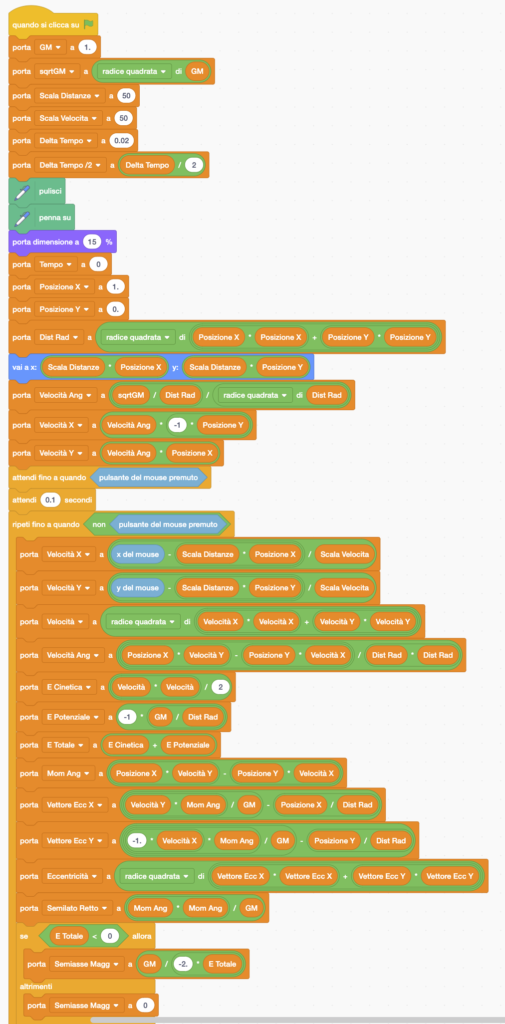
Passiamo ora ad un secondo codice:

Per scaricare il codice, o per eseguirlo, cliccare qui.

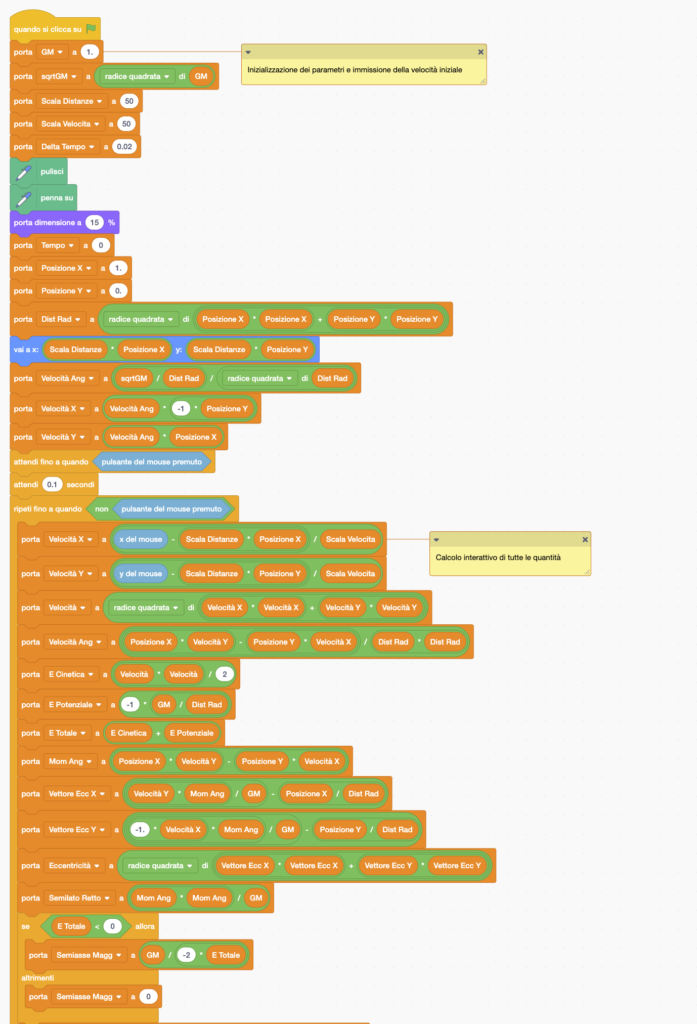
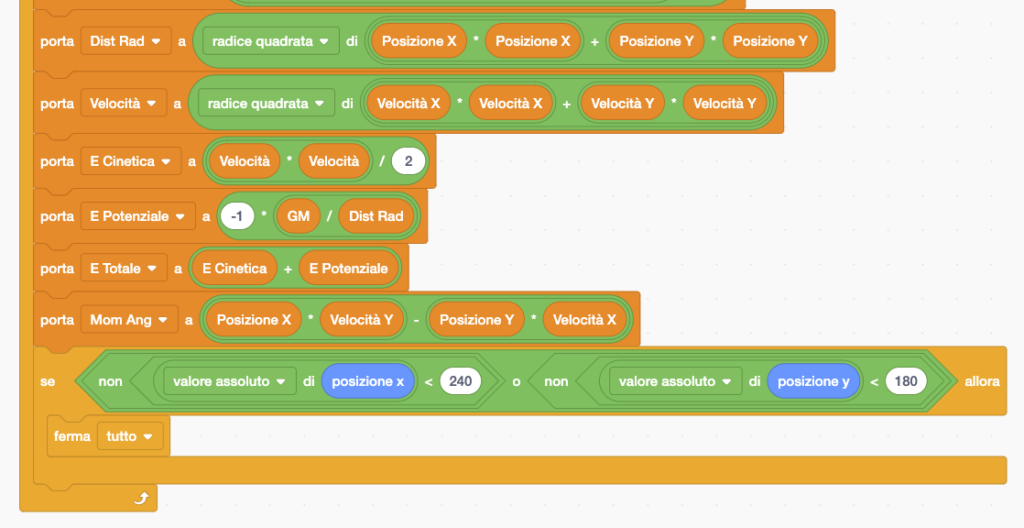
Questo riprende il precedente per quanto riguarda il calcolo del moto orbitale, ma è stato implementato con il calcolo di molte grandezze, sia geometriche che dinamiche. In particolare:

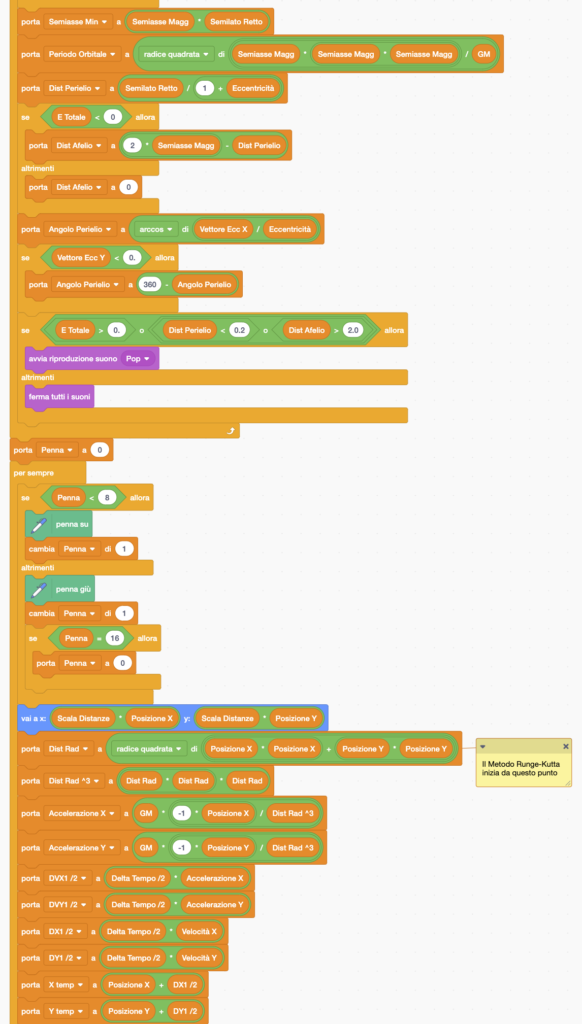
Grandezze geometriche, che identificano la traiettoria dell’orbita: Semiasse Maggiore, Semiasse Minore, Eccentricità, ma anche Distanza dell’Afelio, Distanza del Perielio, Angolo del Perielio (che descrive l’orientazione dell’orbita), Semilato Retto (usato nell’equazione dell’ellisse in coordinate polari).
Quantità dinamiche: Energia Cinetica, Energia Potenziale, Energia Totale, Momento angolare.
E ancora: Distanza Radiale, Velocità, Velocità Angolare, Periodo Orbitale.

Nella versione pubblicata del programma, quasi tutte queste quantità sono visualizzate sullo schermo. Si può facilmente snellire la visualizzazione cancellandole dallo schermo, tuttavia la loro presenza permette di effettuare una serie di interessanti “esperimenti” per verificare alcune proprietà del consequente moto orbitale. Buona parte di queste verifiche si può compiere già durante la fase di impostazione della velocità iniziale, in quanto i parametri dell’orbita nonché i valori iniziali di tutte le grandezze cinematiche e dinamiche sono calcolati in tempo reale, mentre si muove il mouse.

Ad esempio si può notare che:

il periodo dell’orbita dipende solo dal valore del semiasse maggiore (non di quello minore), e che questo a sua volta è funzione dell’energia totale (e non del momento angolare);
il Semilato Retto è funzione del solo momento angolare (e non dell’energia totale);
per i moti chiusi l’energia totale è sempre negativa mentre l’eccentricità è sempre minore di 1;
per i moti aperti (che sarebbero iperboli, invece che ellissi) l’energia totale è positiva mentre l’eccentricità è maggiore di 1. In tale caso le quantità Semiasse maggiore, Semiasse Minore, Distanza dell’Afelio e Periodo Orbitale perdono di significato, e per questo sullo schermo vengono indicati con 0. Da notare invece come anche per le orbite aperte Semilato Retto e Distanza del Perielio mantengono significato.

Al fine di aiutare a immettere velocità iniziali compatibili con orbite chiuse non troppo eccentriche, quando si arriva a parametri iniziali un po’ troppo estremi il programma manda un suono di allerta; comunque se si vogliono immettere valori anche oltre i limiti consigliati, il programma lo consente.

Leggendo il codice si può notare come vengano prima calcolate le componenti del “Vettore Eccentricità” e poi da queste Angolo del Perielio ed Eccentricità. Il Vettore Eccentricità, come il Vettore di Lenz a esso proporzionale, sono grandezze meno note, ma si può vedere come colleghino in maniera elegante proprietà geometriche dell’orbita alla posizione istantanea ed al valore del momento angolare.

Quanto alle grandezze fisiche conservate, si può notare come, nonostante Distanza Radiale e Velocità Angolare possano variare, il Momento Angolare si mantenga costante. Inoltre, nonostante Energia Cinetica ed Energia Potenziale possano variare, l’energia Totale si mantenga costante.

Il fatto che il programma dia per quest’ultima grandezza qualche piccola variazione è un problema puramente numerico, che diventa particolarmente grave se viene scelta un’orbita che passi molto vicino al corpo centrale. L’errore può essere ridotto diminuendo il valore del passo temporale (Delta Tempo), ma per ottenere risultati più accurati (anche se mai del tutto esatti) occorre usare metodi numerici più sofisticati di integrazione dell’equazione del moto.

Per approfondire:

Runge-Kutta: un algoritmo più preciso

Cerchiamo qui di risolvere, o quantomeno mitigare, il problema che si era posto al passo precedente: quello della scarsa accuratezza del metodo numerico usato.

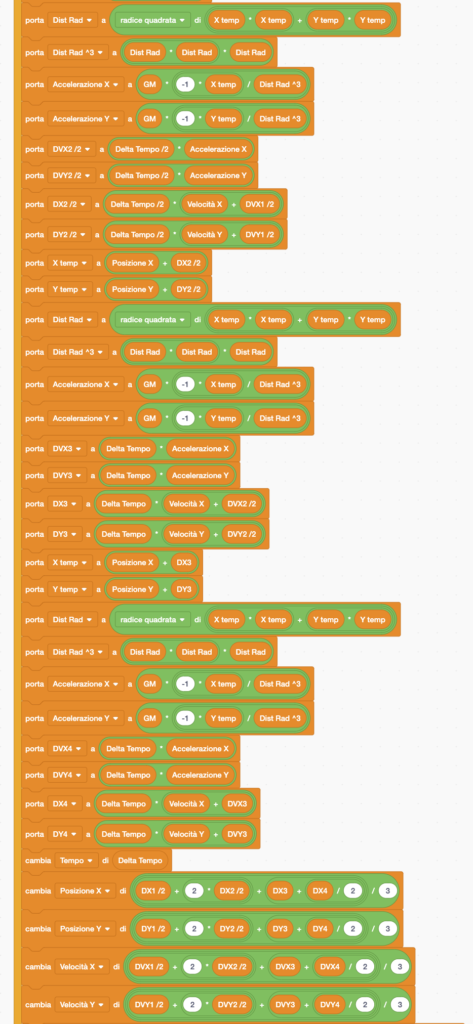
Esistono diversi metodi numerici per integrare numericamente le equazioni di evoluzione nel tempo di un sistema. Purtroppo quelli più efficaci sono anche molto complessi. Qui adotteremo un compromesso, utilizzando un algoritmo ormai classico, sviluppato agli inizi del 1900 dai matematici Carl Runge e Martin Wilhelm Kutta. Lo scopo qui non è di comprendere a pieno questo metodo, ma di introdurlo per poterlo usare successivamente, nel trattare problemi più complessi.

Tuttavia possiamo provare a darne, se non una spiegazione, almeno una motivazione. Consideriamo un’equazione che descrive l’evoluzione di una certa quantità fisica dicendomi quanto essa varia, ad un tempo qualsiasi, ma che però non dipende solo dal tempo ma anche dal valore che questa quantità ha a quel dato tempo. Con una terminologia più matematica si può dire che l’equazione fornisce il valore della derivata temporale di questa quantità, in funzione del tempo e della quantità stessa, l’equazione in questione è detta equazione differenziale.

Per risolvere questa equazione (o meglio 4 equazioni in parallelo, due per le componenti della velocità e due per le componenti della posizione), finora avevamo seguito una procedura abbastanza semplice, calcolando le componenti dell’accelerazione ad un certo tempo, facendo evolvere le componenti della velocità sulla base dell’accelerazione, e quindi facendo evolvere le componenti della posizione sulla base della velocità.

Questo metodo è ovviamente impreciso, perché per calcolare le derivate temporali si usano le condizioni esistenti all’inizio di questo passo temporale, e di fatto si assume che queste non varino durante tutto questo intervallo di tempo, in ché in generale non sarà vero. Tale metodo sarà tanto più preciso quanto più breve sarà il passo temporale scelto, ma questo può allungare a dismisura il tempo di calcolo, senza averne un vantaggio adeguato.

Un metodo per poter seguire meglio l’evoluzione tenendo fissato l’intervallo temporale è quello di provare a prevedere i valori della quantità a tempi successivi a quello d’inizio, e valutare su quelli le derivate temporali che si avrebbero, per poi combinarle assieme ed ottenere una derivata temporale “media” che sia più bilanciata, e che in generale più robusta. Questo, detto in maniera semplice, è quello che fa il metodo di Runge-Kutta o metodi simili.

Ma la migliore motivazione sono i risultati, per cui siete invitati a confrontarli risposto al metodo precedentemente usato: le traiettorie ellittiche sono più stabili, anche dopo molte rivoluzioni, e l’energia totale è molto meglio conservata che nel caso precedente.

Ecco il codice: