Poiché la Prima Legge Keplero recita che il Sole occupa uno dei due fuochi dell’ellisse che descrive l’orbita del pianeta, in questo passo impareremo a tracciare un’ellisse centrata su uno dei suoi due fuochi. Questa sarà anche l’occasione per introdurre altre utili quantità.
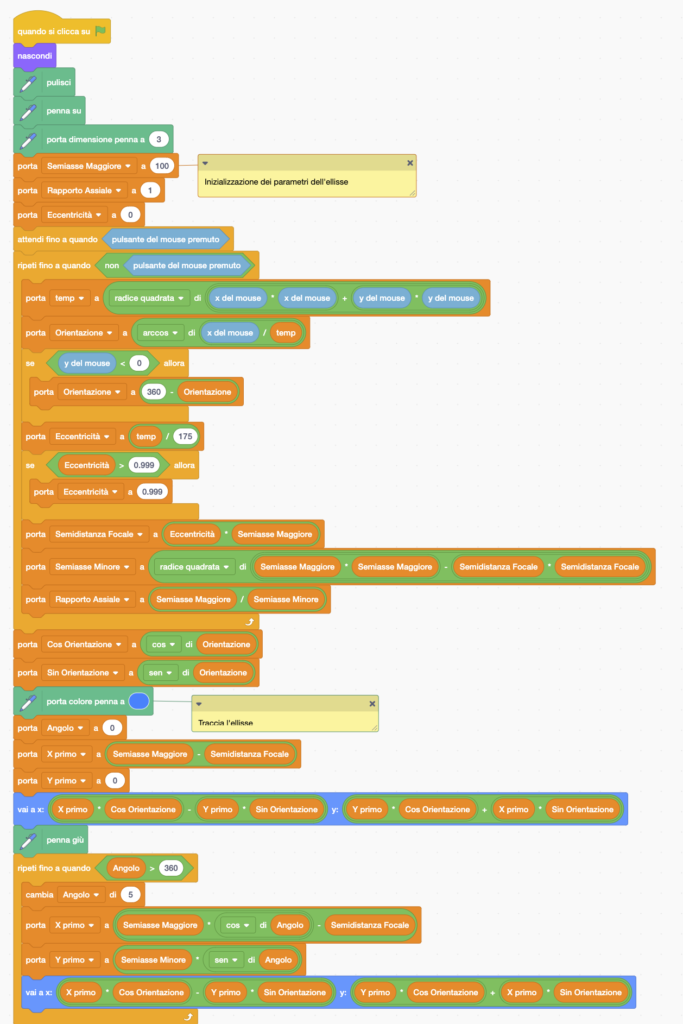
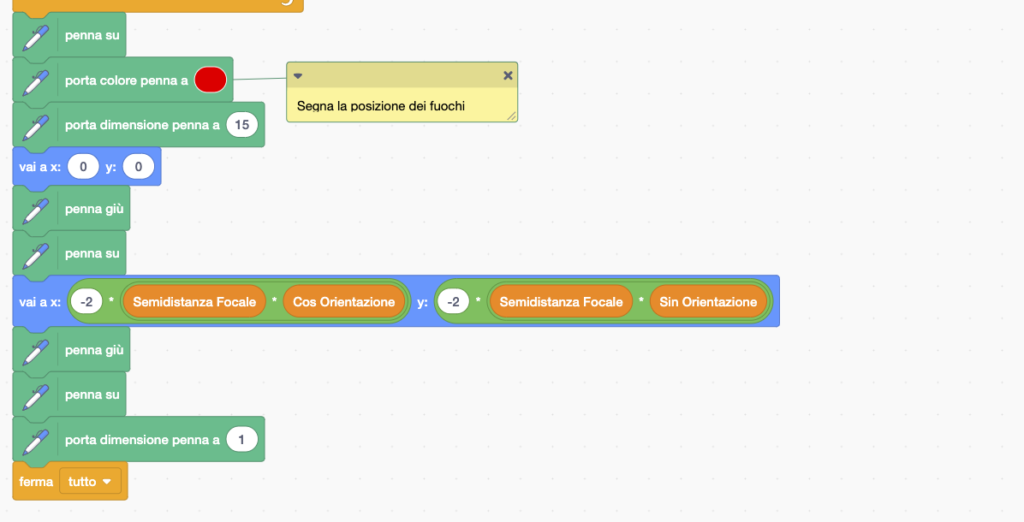
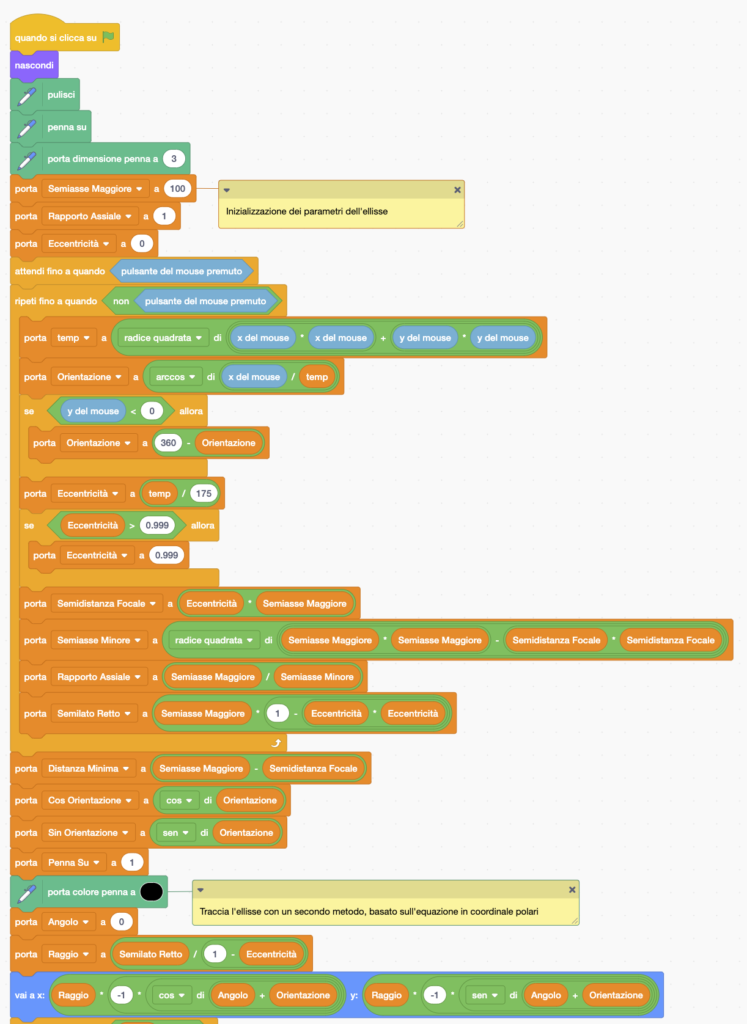
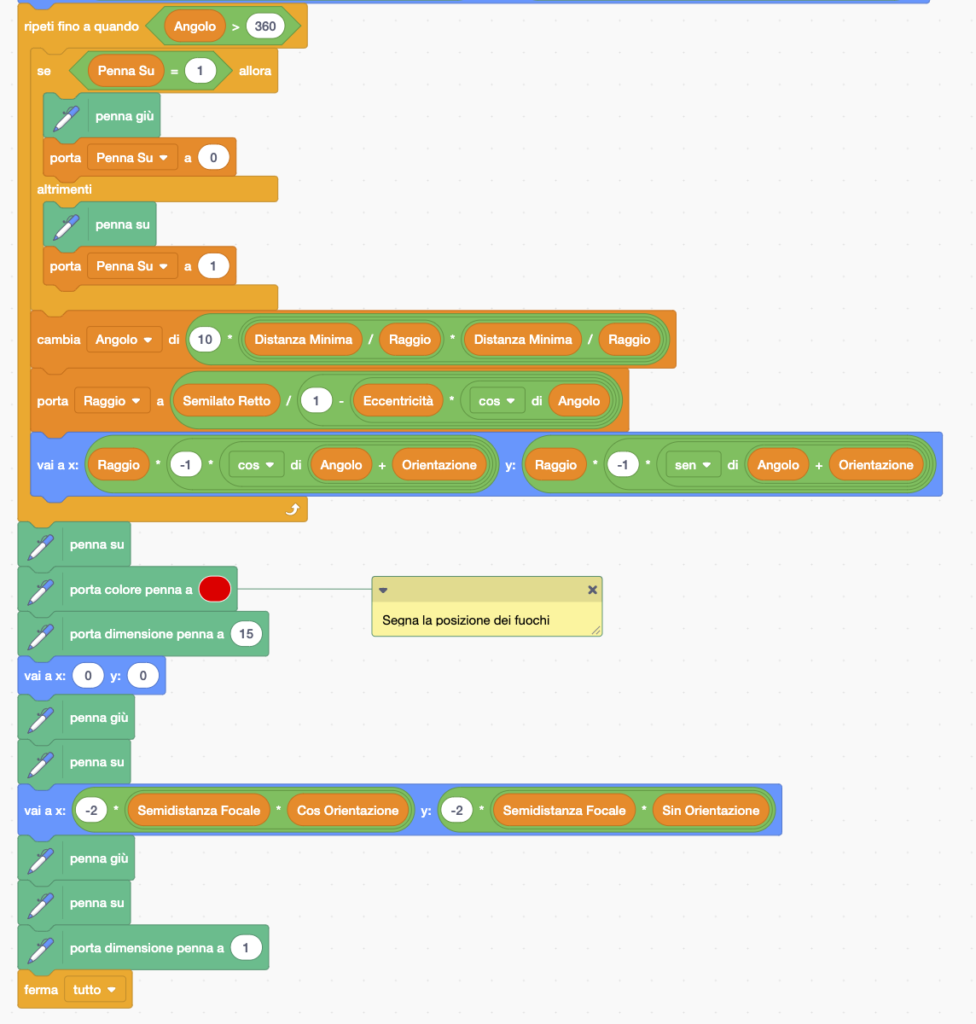
Iniziamo con una versione di codice molto simile all’ultimo presentato nel passo precedente. La differenza principale consiste nell’applicare una traslazione, nel sistema di coordinate ruotate, pari alla metà della distanza assiale, in modo da collocare un fuoco nel centro. Da notare che, con il mouse, viene ora impostata la direzione di minima distanza (perielio).
Ecco il codice Scratch:
Per scaricare il codice, o per eseguirlo, cliccare qui.
Equazione dell’ellisse in coordinate polari
Esiste un altro modo per descrivere matematicamente un’ellisse, in coordinate polari:
![]()
dove la distanza radiale (r) è funzione dell’angolo (θ) a partire dalla direzione perielio. Rivediamo qui l’eccentricità, introdotta precedentemente, ma anche il semilato retto (l) che geometricamente è la lunghezza del segmento perpendicolare all’asse maggiore che unisce un fuoco all’ellisse. Ecco alcune relazioni che legano asse maggiore, asse minore, semilato retto ed eccentricità.
![]()
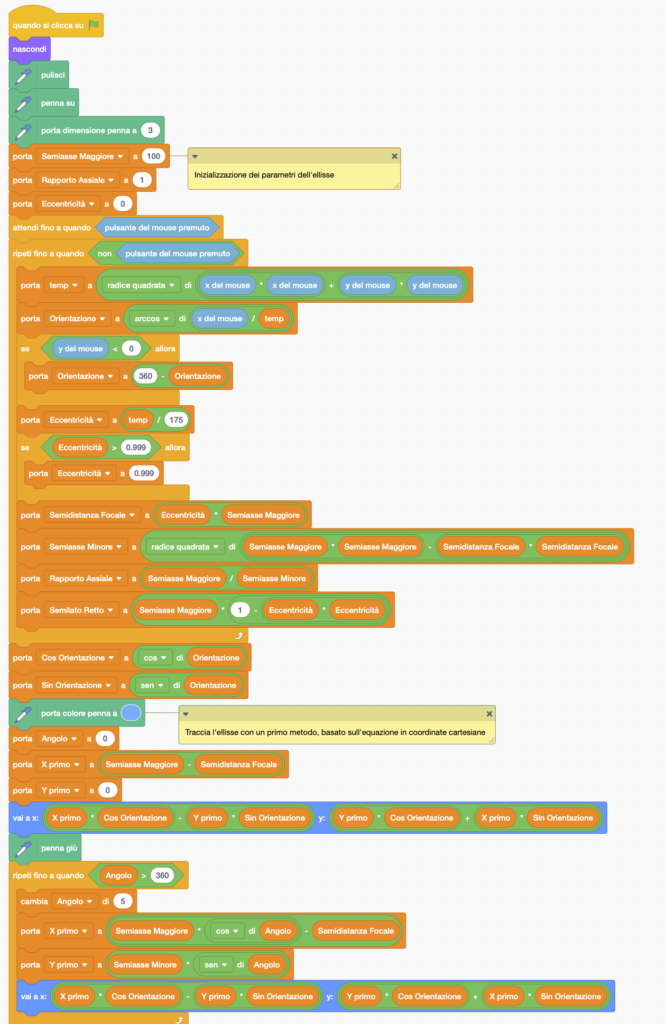
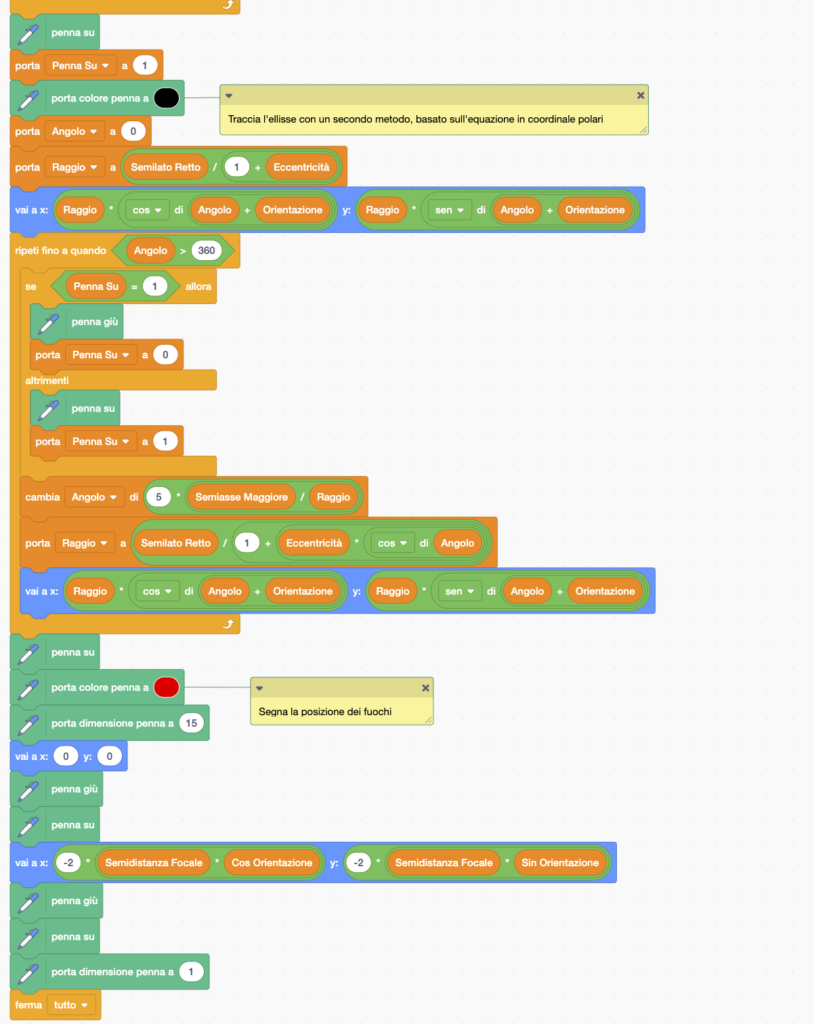
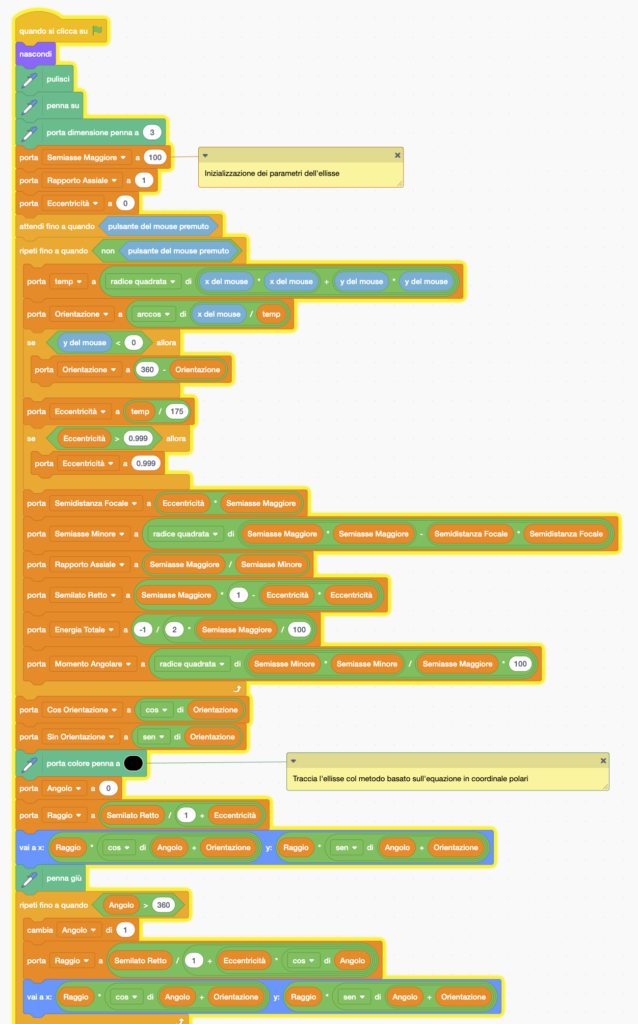
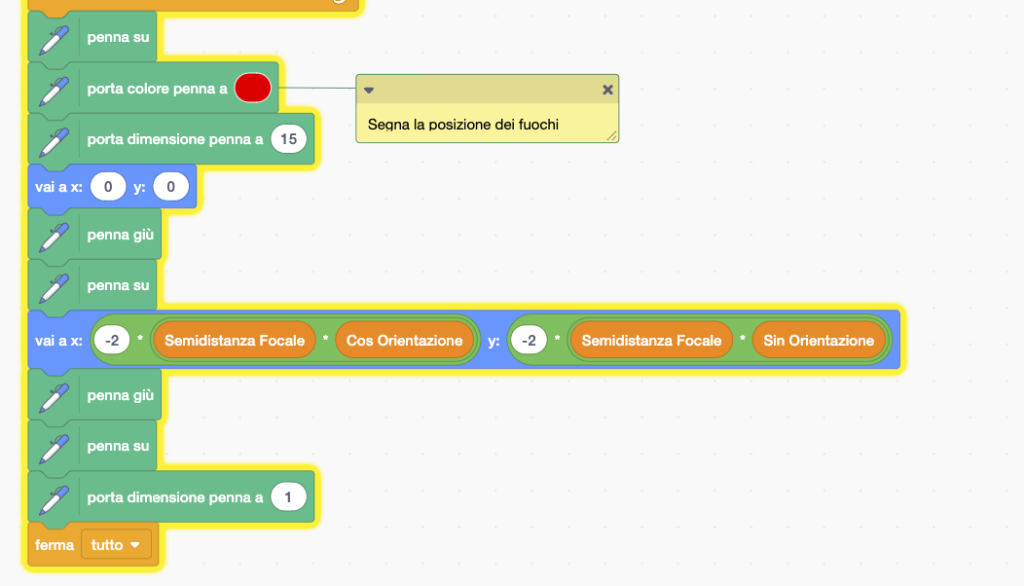
Nel prossimo programma utilizziamo sia il metodo di tracciamento usando la formula in coordinate cartesiane ruotate e traslate (linea continua) che quella iN coordinate polari (linea tratteggiata). Come si può vedere, nonostante i due metodi usati siano molto diversi il risultato è lo stesso. Dal punto di vista del coding, notare come è stato possibile ottenere facilmente una linea tratteggiata, alzando ed abbassando alternativamente la penna ad ogni passo: per far questo si usa una variabile che ricorda se la penna era su o giù al passo precedente, e si inverte di stato ad ogni passo.
Ecco il codice Scratch:
Per scaricare il codice, o per eseguirlo, cliccare qui.
Approssimando la legge delle aree
In questo caso usiamo solo l’equazione dell’ellisse in coordinate radiali. L’unica differenza è che questa volta vogliamo render conto, anche se in maniera approssimata, della Seconda Legge di Keplero (Legge delle aree), in modo che la lunghezza di ogni tratto sia proporzionale alla distanza percorsa nel medesimo intervallo di tempo. Per questo motivo ora ad ogni passo l’incremento dell’angolo è preso inversamente proporzionale al quadrato del valore istantaneo della distanza radiale. Per migliorare il risultato abbiamo usato due piccoli accorgimenti: ora l’ellisse viene tracciata a partire dal punto più distante, dove i tratti sono più corti, in modo da rendere meno visibile il non perfetto accordo tra i tratti stessi; inoltre la quantità che viene impostata è la distanza dei tratti quando la distanza dal centro è minima.
Ecco il codice Scratch:
Per scaricare il codice, o per eseguirlo, cliccare qui.
Introduzione di alcune grandezze fisiche
Finora abbiamo utilizzato unicamente quantità e relazioni geometriche. Visto che nel nostro prossimo passo utilizzeremo una descrizione della dinamica per calcolare un’orbita, qui cominciamo ad introdurre alcune quantità fisiche (Energia Totale E e Momento Angolare L), ed a presentare alcune relazioni che le legano ad alcune entità geometriche (semiasse maggiore e semilato retto) utilizzate in precedenza
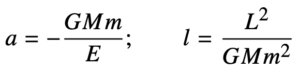
dove m è la massa del pianeta, M quella (molto più grande) del Sole, e G è la costante di gravitazione universale. Come esercizio, da queste due formula, oltre e quelle geometriche mostrate in precedenza, potete provare a derivare anche le formule che legano il semiasse minore (b) e l’eccentricità (e) alle quantità dinamiche introdotte qui sopra. Un altro esercizio consisterà nel derivare le formule semplificate nel caso di un’orbita circolare (e=0).
Per semplicità, nel codice che segue abbiamo posto m=1 e GM=1, ma si tratta solo di una variazione di scale che comunque mantiene la generalità della trattazione. Ecco il codice Scratch
Per scaricare il codice, o per, cliccare qui.
Per approfondire: